Natural frequencies: Faciliting Bayesian inferences

Ana Sofia Morais
Mar 6, 2023

What is the boost?

Unlike conditional probabilities, natural frequencies are not normalized with respect to the base rates. They therefore make it easier for people to apply Bayes’s rule to determine, for instance, how likely it is that a person who tests positive for breast cancer does, in fact, have the disease (i.e., the posterior probability of the disease given a positive test result; Gigerenzer & Hoffrage, 1995).

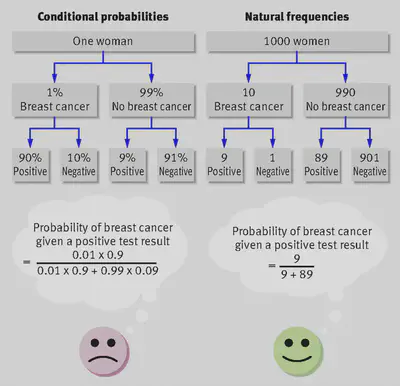
Reprinted from <a href="https://doi.org/10.1136/bmj.d6386" target="_blank">"What are natural frequencies? Doctors need to find better ways to communicate risk to patients," by G. Gigerenzer, 2011, BMJ, 343, Article d6386, p. 2</a>. Copyright 2011 with permission from The BMJ.
Reprinted from “What are natural frequencies? Doctors need to find better ways to communicate risk to patients,” by G. Gigerenzer, 2011, BMJ, 343, Article d6386, p. 2. Copyright 2011 with permission from The BMJ.

The two tree diagrams above summarize the use of mammography to detect breast cancer. The four probabilities on the left are conditional probabilities; the four frequencies on the right are natural frequencies.

Note that natural frequencies are not the same as the normalized frequencies displayed in fact boxes. Natural frequencies carry information about the prevalence of an event (e.g., a disease), while normalized frequencies do not.

Which challenges does the boost tackle?

Conditional probabilities require people to apply a complex Bayesian algorithm to determine a test’s positive predictive value (i.e., Bayes’ theorem). This is because the information about the prevalence of, for instance, a disease, has to be reintroduced by multiplying it by each conditional probability. There is abundant evidence showing that people have difficulty carrying out these computations (see literature review in McDowell & Jacobs, 2017).

Which competences does the boost foster?

Natural frequencies simplify computations and specify the pieces of numerical information and how they relate to each other. They thus help people make Bayesian inferences, which are more difficult to make based on conditional probabilities. The improvement in performance is a short-term, “local fix,” that is, there is no aspiration to improve Bayesian reasoning beyond the current context.

What is the evidence behind it?

A meta-analysis showed that, on average, 24% of participants correctly solved Bayesian inference problems in the natural frequency format, whereas only 4% did so in the conditional probability format. These proportions imply an odds ratio of 7.1, which can be considered a strong effect (McDowell & Jacobs, 2017).

Key references

Risk Literacy